티스토리 뷰
안녕하세요.
현대대수학1을 수강해서 수업내용을 토대로 정리한 것을 복습하는 목적으로 글을 쓰려고 합니다.
한마디로... 현대대수학 '고수'되기 프로젝트 입니다!
같이 가보시죠...!
1. 이진 연산(Binary Operation)이란?
이진 연산은 두 개의 값을 받아서 하나의 값을 반환하는 연산을 의미합니다.
수학에서는 주로 * 기호를 사용하여 나타냅니다.
예를 들어, 덧셈(+)과 곱셈(×)도 이진 연산입니다.
만약 어떤 집합 R 위에서 * 연산이 정의되었다면, 우리는 이를 (R, *)라고 표기합니다.
즉, (R, *)는 집합 R에서 *라는 연산을 사용하여 연산을 할 수 있다는 뜻입니다.
Binary Operation은 다음 5가지 조건들을 만족합니다.

2. 그룹(Group)이란?
그룹은 하나의 집합과 하나의 연산이 결합된 구조입니다.

그룹이 되기 위한 조건
그룹이 되려면 다음 네 가지 조건을 만족해야 합니다:
- 닫힘성(Closure): 그룹 안의 원소끼리 연산하면 결과도 그룹 안에 있어야 합니다.
- 결합법칙(Associativity): 연산을 할 때 괄호를 바꿔도 결과가 동일해야 합니다.
- 즉, (a * b) * c = a * (b * c)가 항상 성립해야 합니다.
- 항등원(Identity Element) 존재: 연산을 해도 변하지 않는 값(항등원)이 있어야 합니다.
- 예) 덧셈에서는 0, 곱셈에서는 1
- 역원(Inverse Element) 존재: 모든 원소 a에 대해 a * a⁻¹ = 항등원을 만족하는 원소 a⁻¹이 존재해야 합니다.
그룹의 종류
| Semigroup | 닫힘성 + 결합법칙 |
| Monoid | Semigroup + 항등원 존재 |
| Group | Monoid + 역원 존재 |
| Abelian Group(= Commutative Group) | Group + 교환법칙 성립 (a * b = b * a) |
📌 암기 TIP: 저는 이 순서를 클어아인커라고 외웠어요!
클어아인커 → (클) 닫힘성, (어) 결합법칙, (아) 항등원, (인) 역원, (커) 교환법칙
뒷 내용을 설명할때 클어아인커를 자주 언급할겁니다.
Abelian Group vs Commutative Group
둘 다 같은 개념이지만, 관례적으로
- 곱셈 연산을 사용하면 Commutative Group
- 덧셈 연산을 사용하면 Abelian Group 이라고 부르는 경우가 많습니다.
3. 링(Ring)이란?
링은 하나의 집합과 두 개의 연산(보통 덧셈과 곱셈)이 있는 구조입니다.

링의 기본 조건
- 덧셈 연산(+)이 Abelian Group이어야 합니다.
- 곱셈 연산(×)이 닫혀있어야 합니다.
- 곱셈 연산과 덧셈 연산이 분배법칙을 만족해야 합니다.
- (a + b) × c = (a × c) + (b × c)
- c × (a + b) = (c × a) + (c × b)
이 조건들을 만족하면 R은 Ring(링)입니다!
4. 부분 그룹(SubGroup)이란?
부분 그룹은 부분 집합과 비슷한 개념입니다.
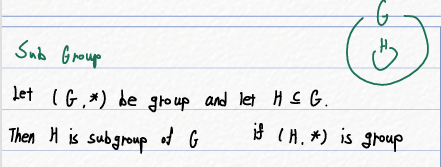
부분 그룹의 조건
어떤 H가 그룹 G의 부분 그룹이 되려면:
- H는 G의 부분 집합(Subset)이어야 한다.
- H가 G의 연산을 그대로 따라야 한다.
쉽게 말해, 그룹 G의 일부 원소를 가져와서, 이 원소들끼리 연산을 해도 그룹의 성질이 유지되면 그것이 부분 그룹입니다!
5. 순환 부분 그룹(Cyclic SubGroup)
순환 부분 그룹은 하나의 원소로 생성되는 부분 그룹을 의미합니다.
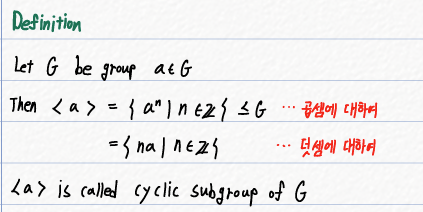
어떤 그룹 G의 원소 a가 주어졌을 때, a의 모든 거듭제곱(혹은 덧셈 그룹에서는 배수)으로 생성되는 집합을 ⟨a⟩라고 합니다. 이 ⟨a⟩가 G의 부분 그룹이라면, 우리는 이를 순환 부분 그룹(Cyclic SubGroup)이라고 부릅니다.
+Notation) # = The number

기호 부분인데, 그룹에 절댓값 표시를 하면 원소의 개수를 뜻합니다.
6. 생성원(Generator)과 순환 그룹(Cyclic Group)
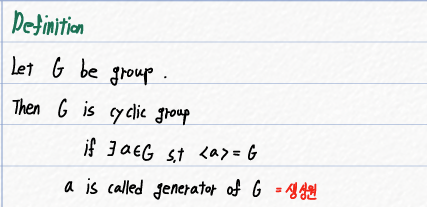
어떤 그룹 G가 단 하나의 원소로부터 만들어질 수 있다면, G를 순환 그룹(Cyclic Group)이라고 합니다.
그리고 그 한 개의 원소를 생성원(Generator)이라고 합니다.
몇가지 예제를 살펴보겠습니다.
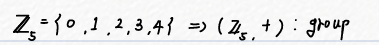
이 친구는 덧셈 연산자에 대하여 group입니다.
이 그룹에서 적당한 원소를 뽑아보겠습니다.
저는 2를 선택했습니다. 이제 <2>를 구해보죠!
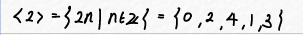
<2> 를 구해봤더니 \(Z_5\)와 동일합니다.
그렇다면,
\(Z_5\) 는 Cyclic Group이고, 2는 \(Z_5\) 의 생성원 입니다!
3에 대해서도 살펴보겠습니다.
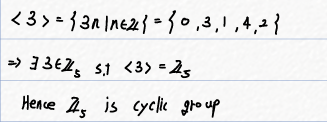
3도 \(Z_5\)의 생성원임을 알수 있습니다.
모든 원소에 대해서 생성원인지 아닌지 확인하는 것은 너무 귀찮습니다.. 그래서!
생성원을 빠르게 찾는 방법을 알려드리겠습니다!
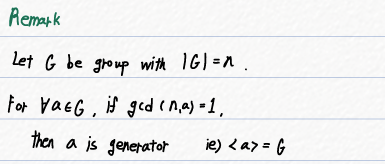
그룹 G의 원소의 개수를 n 이라고 했을 때, G의 원소를 하나 택해서( a라고 하겠음.)
gcd(a,n) = 1이라면, a는 generator입니다.
\(Z_6\)에 대해서 살펴보겠습니다. \(Z_6\)은 다음과 같은데요.
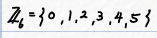
원소의 개수는 6개 입니다. => n = 6
a를 \(Z_6\)의 원소라고 할때 gcd(a,6) = 1을 만족하는 a는 무엇이 있을까요?
만족하는 a는 1과 5입니다.
따라서 \(Z_6\)의 생성원은 1과 5 두개입니다!
6. 클라인 4원군(Klein 4-Group)
클라인 4-원군(K₄)은 아주 중요한 예제입니다.
그냥 그룹의 예제 인줄알았는데, GPT피셜 중요하답니다....ㅠ
클라인 4-원군의 연산은 아래와 같습니다. (아래의 연산은 *이라 하겠습니다)
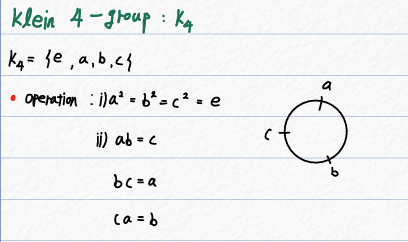
(\(K_4\),*)이 Group인지 확인해 봅시다.
Group은?
클어아인 << 이것만 보이면 됩니다.

*연산을 보면 어렵지 않게 Group이라는 것을 알수 있습니다.
갑자기 궁금증이 생기네요. Klein 4-Group은 Cyclic Group이 될까요??
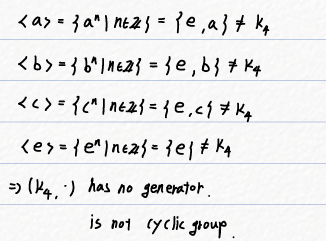
아쉽게도, 모든 원소 하나하나 살펴봐도 없습니다.. Cyclic Group이 아니에요.
하지만!
ab = c = ec = \(b^2\)c = (bb)c = b(bc) = ba 이기 때문에 교환법칙이 성립합니다.
Klein 4-Group은 Cyclic Group이 아니지만 Abelian Group이네요!
---
## 📌 관련된 Theorem 정리
1) ⟨a⟩는 G의 부분 그룹이다.
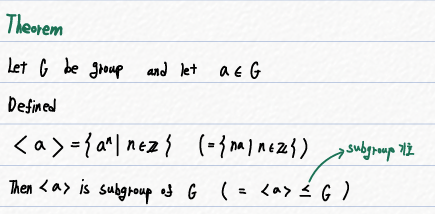

어떤 원소 a로 생성된 순환 부분 그룹 ⟨a⟩가 G의 부분 그룹임을 증명하기 위해 두 가지 조건을 확인해야 합니다.
- ⟨a⟩가 G의 부분 집합(SubSet)인지 확인
- ⟨a⟩의 임의의 원소를 선택하여 G의 원소임을 증명하면 됩니다.
- ⟨a⟩가 G의 연산자에 대해 그룹인지 확인
- ⟨a⟩가 G의 연산 아래 그룹을 이루는지 보이려면,
- 닫힘성(Closure)
- 결합법칙(Associativity)
- 항등원(Identity Element) 존재
- 역원(Inverse Element) 존재
- 닫힘성은 자명하므로, 나머지 조건들만 확인하면 됩니다.
- (증명에서는 곱셈 연산을 사용했지만, 덧셈 연산이라면 ⟨a⟩ = {na | n ∈ 정수}로 표현할 수 있습니다.)
- ⟨a⟩가 G의 연산 아래 그룹을 이루는지 보이려면,
2) G의 순환 부분 그룹은 항상 아벨 그룹이다.
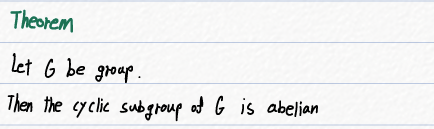
G가 Group일때, G의 Cyclic SubGroup은 abelian 이라는 정리입니다.
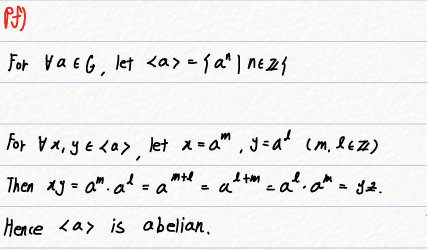
증명은 다음과 같이 진행됩니다.
- Abelian(교환법칙 성립) 여부를 확인하기 위해 클어아인커 조건을 따져봅니다.
- 순환 부분 그룹은 이미 그룹(SubGroup의 정의를 따름)이므로 클어아인을 보일필요가 없습니다, 교환법칙(Commutativity) 만 보이면 충분합니다.
- 즉, 임의의 ⟨a⟩의 원소 \(a^m\) , \(a^n\)에 대해 연산이 \(a^m\) * \(a^n\) = \(a^n\) * \(a^m\)를 만족하면, 이는 항상 성립하므로 ⟨a⟩는 Abelian Group입니다.
3) H가 G의 부분 집합일 때, 다음이 성립한다.
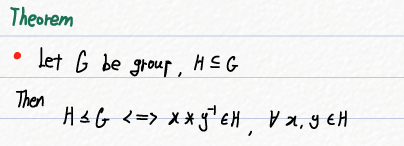
H가 G의 부분 그룹이다. ⇔ x * y⁻¹이 H의 원소이다.
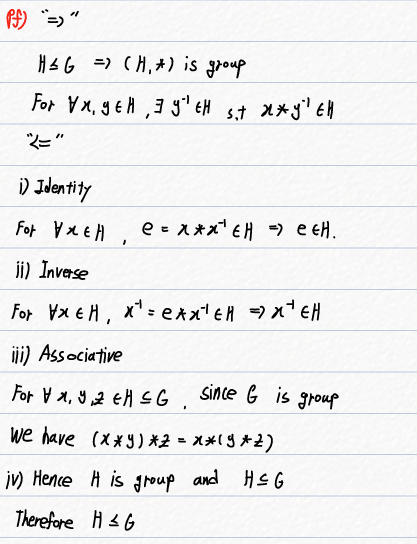
H가 G의 SubGroup이라는 것과 x * y⁻¹이 H의 원소임이 동치라는 것을 보이겠습니다.
증명:
(⇒ 방향)
- H가 G의 SubGroup이라 가정하면, H는 그룹이므로 클어아인을 만족합니다.
- 따라서 H의 모든 원소는 역원을 가지므로 y⁻¹ ∈ H입니다.
- 또한 닫혀있기 때문에 x * y⁻¹ 역시 H의 원소입니다.
(⇐ 방향)
- 반대로 x, y ∈ H일 때 x * y⁻¹ ∈ H라고 가정합니다.
- H가 그룹인지 증명하려면, 클어아인을 만족해야 하므로 다음을 확인합니다.
- 닫혀있음은 자명하므로 생략합니다.
- 항등원: x = y일 경우 x * y⁻¹ = e이므로 e ∈ H.
- 역원 존재: x⁻¹ = e * x⁻¹ = (x * x⁻¹) * x⁻¹ = e * x⁻¹ = x⁻¹ ∈ H.
- 결합법칙은 G에서 성립하므로, H에서도 성립합니다.
따라서, x * y⁻¹이 H에 속하는 것과 H가 G의 SubGroup인 것은 동치임을 증명할 수 있습니다.
이렇게 현대대수학의 1주차 내용을 정리해 보았습니다!
저도 현대대수는 처음이라서 잘못된 부분이 있거나 더 궁금한 점이 있다면, 언제든지 댓글 남겨주세요!
- Total
- Today
- Yesterday
- cyclicgroup
- 티스토리챌린지
- raw회전이동
- activationfunction
- fashionMNIST
- 정보전송
- MLP
- 신경망딥러닝
- bmptoraw
- BMP
- 회전이동
- 의류분류
- bias
- sungroup
- generator
- 영상처리 #기초
- DEEPLEARNING
- bmp헤더
- 다층퍼셉트론
- perceptron
- errorcorrecting
- klein4group
- errordetecting
- 편향
- RAW
- 오블완
- 현대대수학
- 퍼셉트론
- 활성화함수
- rawtobmp
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
